Visual Maths: Number System
Imagine a machine which is nothing more than a row of boxes that extends as far to the left. Let’s call it a “two-one machine” both written and read in a funny backwards way.
And what do you do with this machine? You put in dots. Dots always go into the rightmost box.
- Put in one dot, and, well, nothing happens: it stays there as one dot.
- But put in a second dot – always in the rightmost box – and then something exciting happens. Whenever there are two dots in a box they explode and disappear – Bhoom! – to be replaced by one dot, one box to the left.
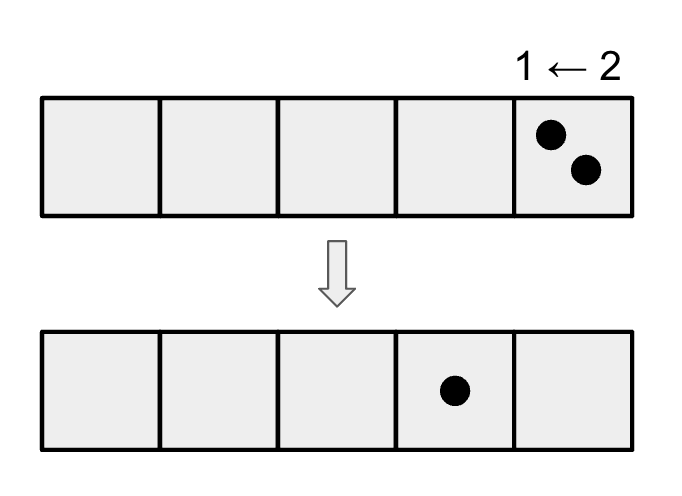
We see that two dots placed into the machine yields one dot followed by zero dots.
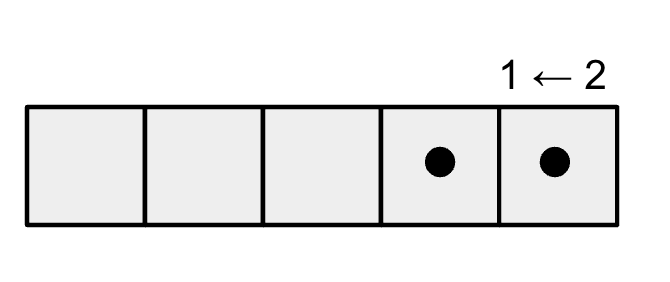
Putting in a third dot – always the rightmost box – gives the picture one dot followed by one dot.
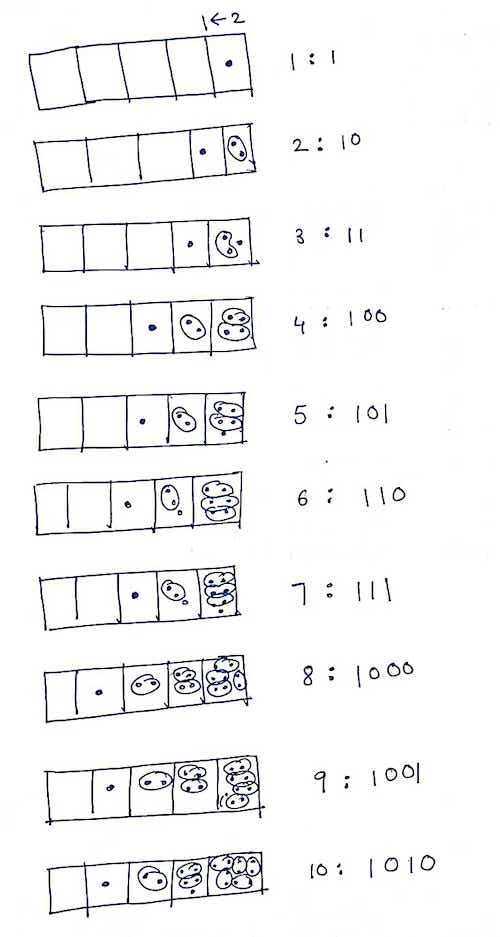
Let’s make a table and do it for all numbers till 10
| Numbers | 1 <- 2 |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
Here is a visual way to look at it
Now, instead of playing with a 1 <- 2 machine, we could play with a 1 <- 3 machine (again
written and read backwards, a “three-one “machine). Now whenever there are three dots in a
box, they explode away to be replaced with one dot, one box to the left.
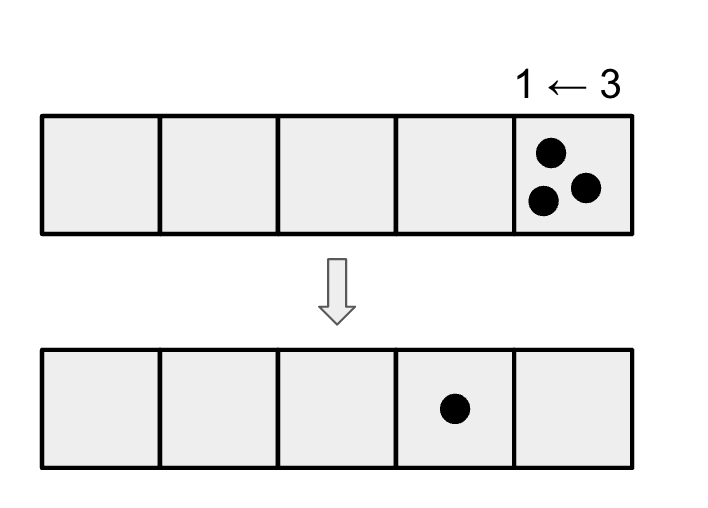
| Numbers | 1 <- 3 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 10 |
| 4 | 11 |
| 5 | 12 |
| 6 | 20 |
| 7 | 21 |
| 8 | 22 |
| 9 | 100 |
| 10 | 101 |
You can try this for different types of machine: 1 <- 4, 1 <- 5 and so on…
What are these machines doing?
Can you figure out what these machines are actually doing? Why is the code for two hundred and seventy-three in a 1 <- 10 machine, “273”? Are all the codes for numbers in a 1 <- 10 sure to be identical to how we normally write numbers. If you can answer that question, can you then also make sense of all the codes for a 1 <- 2 machine? What does the code 1101 for the number thirteen mean?
Both the above approaches, teaches the concept of binary (1 <-2) , tertiary (1 <- 3) and decimal (1 <- 10) number systems.
 Copied
Copied
